$\require{color}$

Mesh Modification

Two types of topology (i.e. connectivity):

• Mesh connectivity
• Surface connectivity

Hence mesh modification is geometric (i.e. no changes to mesh connectivity but can change underlying surface.)

• UV map
• Smoothing
• Note: possible to destroy topology!

Whereas surface modification is topological (i.e. no changes to the underlying surface, but allow changes within mesh connectivity.)

.Underlying space: “the structure” of the object.

Vertex insertion

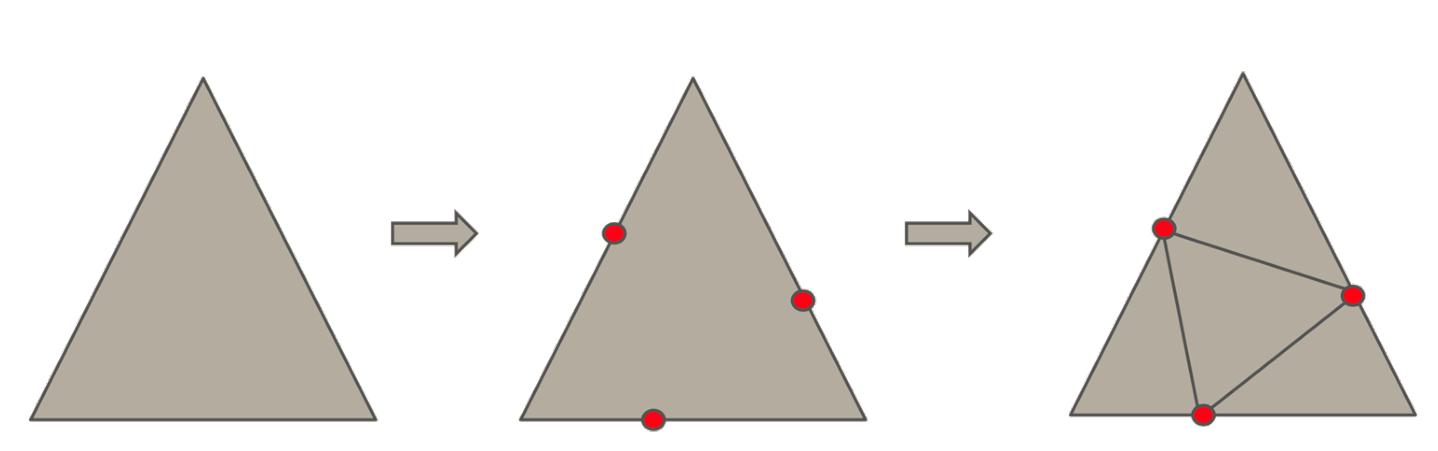
A new vertex can be inserted onto

• a triangle
• an edge
• an existing vertex (bad!)

Barycentric subdivision

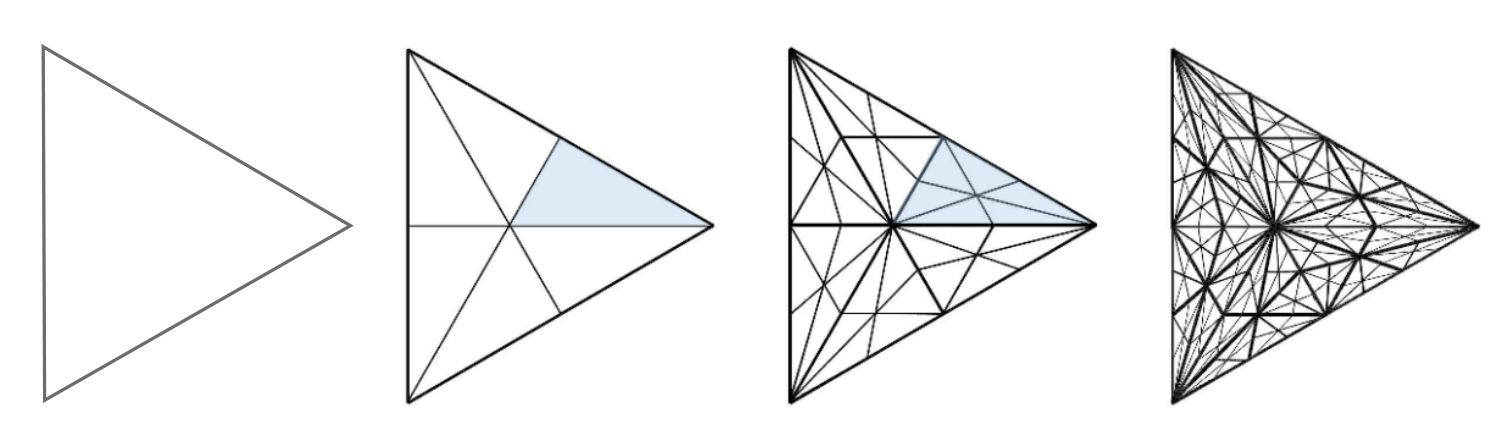
Recursively subdivide into 6 triangles (angles get very small but mathematically easy to do.)

A type of vertex insertion; new vertices are inserted into the centroid of the subdivided triangles.

Loop subdivision

Add a vertex to each edge and cut. Can be done with and without smoothing.

Partial Barycentric

Edge swapping

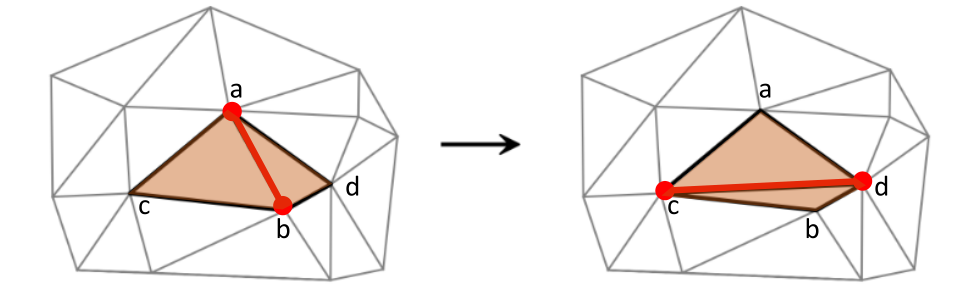
Delete 2 triangles and add the opposite edge, recreating two triangles. Used for mesh refining

Edge contraction

• Merge two adjacent vertices
• Delete two original triangles and extra edges
• Stitch the empty hole

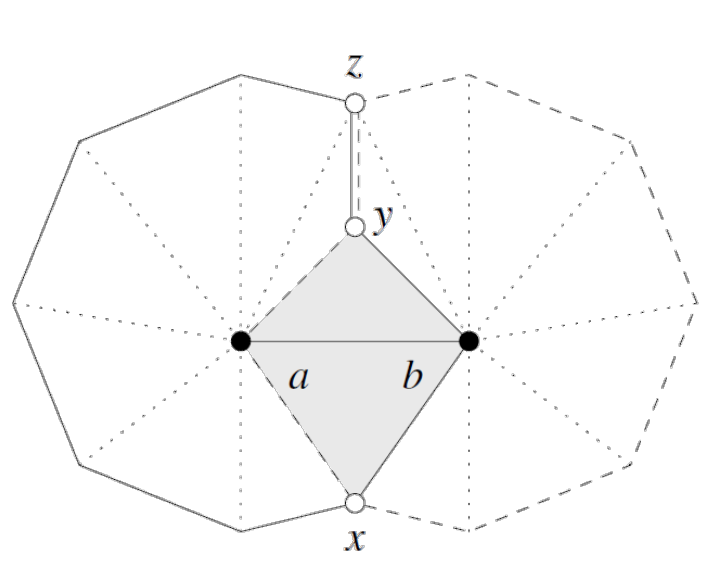
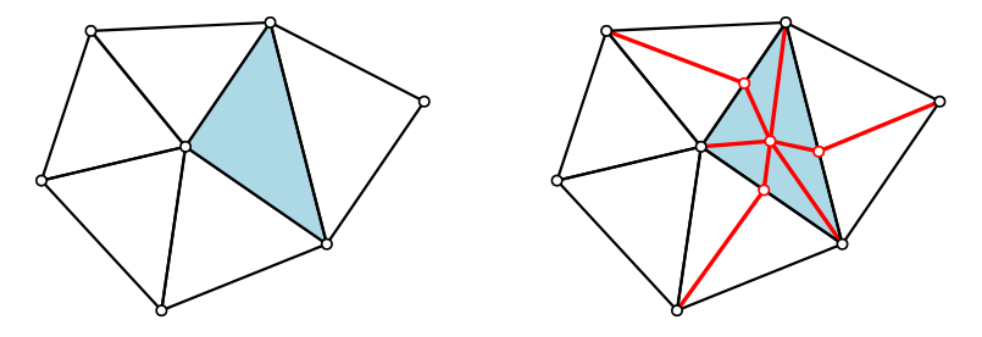
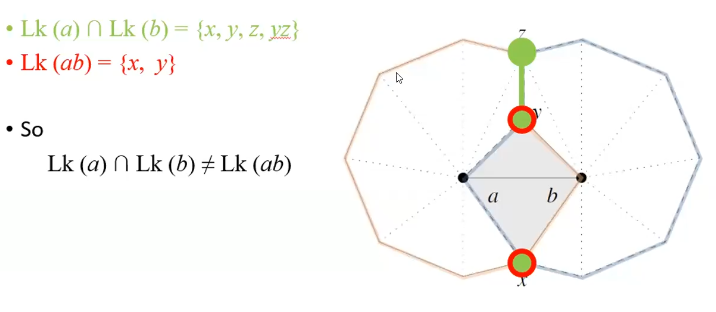
BE CAREFUL! A contractible edge $ab$ must satisfy $\textcolor{red}{Lk(a) \cup Lk(b) = Lk(ab)}$​.

$Lk$ is the link function​.

• $Lk(v)$​ where $v$​ is a vertex: All the neighbouring vertices and surrounding edges (not edges connected to) of $v$​.
• $Lk(uv)$​ where $uv$​ is an edge: All the vertices on neighbouring triangles excluding $u$​ and $v$​.

These are sufficient, other operations are a combination of the above. How to do these efficiently?

Self-intersection

Any operation that moves vertices/edges can cause self-intersection. However we often want our model to be water-tight (closed manifold with no-intersection)

Simplex

A set of points $S$ is affinely independent if any point $x$ in $S$ is not a linear combination of $S \setminus {x}$​.

A set of vectors is affinely dependent if there are more vectors than necessary to generate their affine hull.

• -1 simplex: empty set.
• 0 simplex: point
• 1 simplex: line
• 2 simplex: triangle
• 3 simplex: tetrahedron
• The convex hull of $d$ affinely independent points is called a d-simplex.
• Given any $T \subseteq S$​​, where $S$​ is the set of points forming the simplex $\sigma$​, the simplex generated by $T$​ is called a face of $\sigma$​​.

Simplicial Complex

A simplicial complex is a set $K$ of simplices that must satisfy:

1. Every face of a simplex in $K$​ also belongs to $K$​
2. For any two simpleices $\sigma_1, \sigma_2$​ in $K$​, if $\sigma_1 \cap \sigma_2$​ is non-empty, then $\sigma_1 \cap \sigma_2$​ is a common face of both $\sigma_1, \sigma_2$​.

Edge contraction Math Explanation

Given simplicial complex $K$ and a subset $S \subseteq K$:

• Star: set of all the simplices in $K$ such that each simplex has a face in $S$.
  • Idea: all simplices that “contains” any simplex in $S$
• Closure: set of all faces of the simplices in $S$​.
  • Idea: the simplices formed by every subset of the points in $S$.
• Link: $Lk(s) = Cl(St(S)) - St(Cl(S))$
  • Idea: All the faces of the simplices containing $S$​​, except the simplices themselves.

Below illustrates $Lk(a)$ and $Lk(ab)$. A contractible edge $ab$ must satisfy $\textcolor{red}{Lk(a) \cup Lk(b) = Lk(ab)}$.

Triangle intersection

No self intersection = mesh is a simplicial complex.

Given 2 triangles, how do we tell if 2 triangles are intersecting?

How to check in a mesh with $n$ vertices for intersections?

Naive: Brute force checking every pair of triangles $O(n^2)$.

More efficient: We can use binary search trees to partition the triangles into pairs.

• kd-trees (3D): Given a triangle, we use its bounding box and range search on the 3d-tree.
  • $k$ intersections, $n$ triangles
  • $O(n^\frac{1}{3} + k)$ time
• Octree: finds the bounding box of a mesh. Adaptive method that stops cutting a region when there’s very few vertices in it.
  • Take median and partition points into left and right of the median plane.
  • If number of triangles (shouldn’t it be vertices) exceed certain number, subdivide into 8 cubes

These more efficient methods reduce the number of triangles we have to brute-force compare on.

If 2 triangles share a common edge, we don’t consider them as intersecting (we can detect by checking the fnexts).

Precision

Imprecise calculations are bad. Heuristic epsilons, interval arithmetic don’t cut it.

Exact arithmetic

• Based on Long integers
• Allowed operations: $+, -, \times$
• Disallowed: $\div, \sqrt{}$​​
• Non-integer values are represented as combinations of arithmetic operations

Geometric Computation

Mostly in terms of predicates. e.g. Given 3 points, return if case is turn left, turn right or collinear.

• Left turn test. Suppose we have points $a,b, c, \in \mathbb{R}^3$
• $abc$​​ is a left turn if the cross product $cb_{xy} \times ba_{xy}$​​​​ has positive z-value

Computation: $\begin{aligned} & \det(\left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ x_c - x_b & y_c - y_b & 0 \\ x_b - x_a & y_b - y_a & 0 \\ \end{matrix} \right|) \\ & = \left|\begin{matrix} x_c - x_b & y_c - y_b \\ x_b - x_a & y_b - y_a \\ \end{matrix} \right| \mathbf{k} \\ & = \frac{1}{2} \left| \begin{matrix} x_a & y_a & 1 \\ x_b & y_b & 1 \\ x_c & y_c & 1 \\ \end{matrix} \right| \mathbf{k} \quad \textcolor{red}{\text{(SignedArea(a, b, c))}}\\ &\ge 0 \end{aligned}$

Line segment intersection

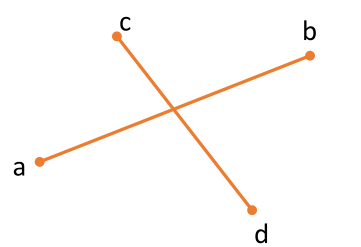
a, b on opposite sides of c,d. and c, d on opposite sides of a, b.

$\Rightarrow$ abd is a opposite handed turn of abc, and cda is an opposite handed turn of cdb

$\Rightarrow \text{SignedArea}(a,b,d) \cdot \text{SignedArea}(a,b,c) <0$​​​​ AND $\text{SignedArea}(c,d,a) \cdot \text{SignedArea}(c,d,b)<0$​​​​

Degeneracy

When predicates (signed area) yield zero.

Incircle test

Speeding up Exact arithmetic

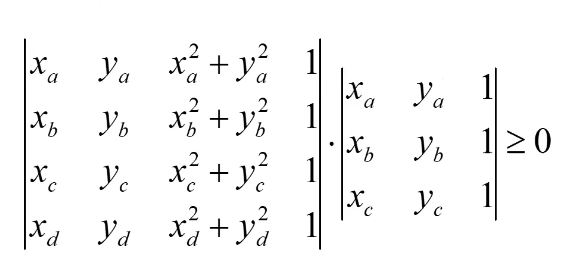
Arithmetic filter: only do exact arithmetic computation when falls within a certain epsilon of 0.