Rotation

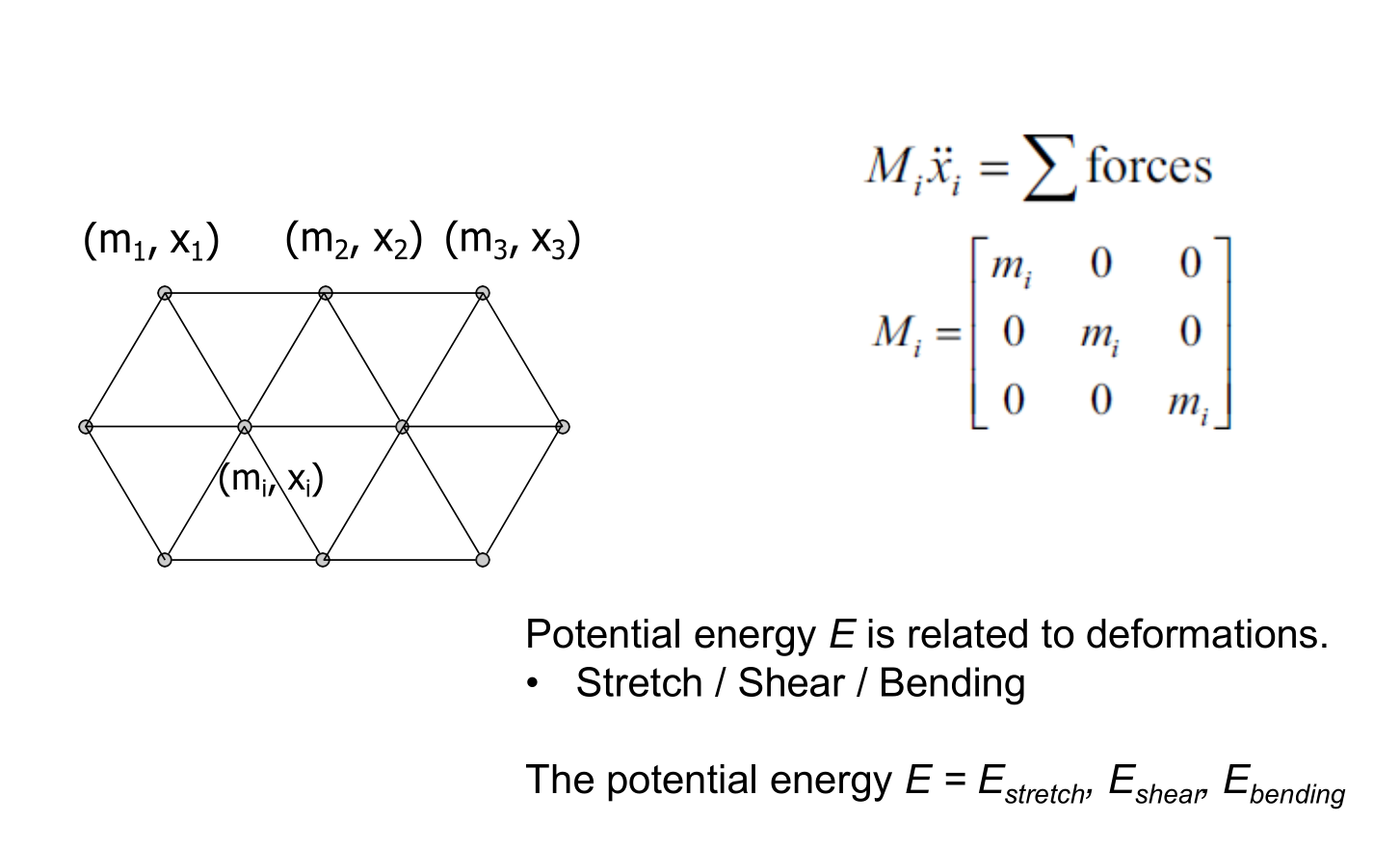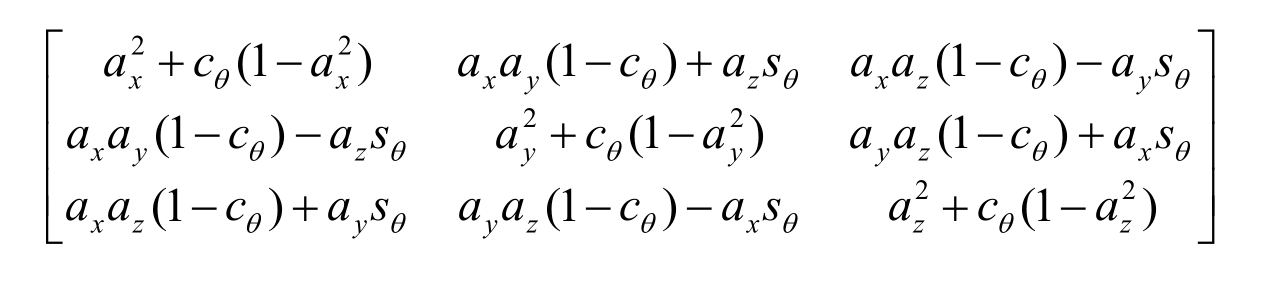
Counter clockwise (right hand rule with thumb on arrow side) is positive.

Rotation Matrix

\[\begin{aligned} Q_x &= \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \\ \end{matrix} \right]\\ Q_y &= \left[ \begin{matrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \\ \end{matrix} \right]\\ Q_z &= \left[ \begin{matrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]\\ \end{aligned}\]

Important Case: Rotate axis $(0, 0, 1)$ to $(1, 1, 1)$

Multiply two rotation matrices together and work out what the angles $\alpha$ and $\theta$ are.

Axis-angle

Rotate about axis $a$ by angle $\theta$.

Important Case: Rotate axis $(0, 0, 1)$ to $(1, 1, 1)$

Axis of rotation = normalize(target vector $\times$ orig vector)

\[\begin{aligned} & \text{norm}(a_f \times a_0) \\ &= \text{norm}((1, 1, 1) \times (0, 0, 1)) \\ &= (1, -1, 0) / \sqrt{1^2 + (-1)^2 + 0} \\ &= (\sqrt{1/2}, -\sqrt{1/2}, 0) \end{aligned}\]

Angle of rotation = $\cos^{-1}$(unit target dot unit orig)

\[\cos\theta = \hat{a}_t \times \hat{a}_0 = \sqrt{1/3}\\ \sin\theta = \sqrt{1 - \cos^2(\theta)} = \sqrt{2/3}\]

Substitute into the matrix:

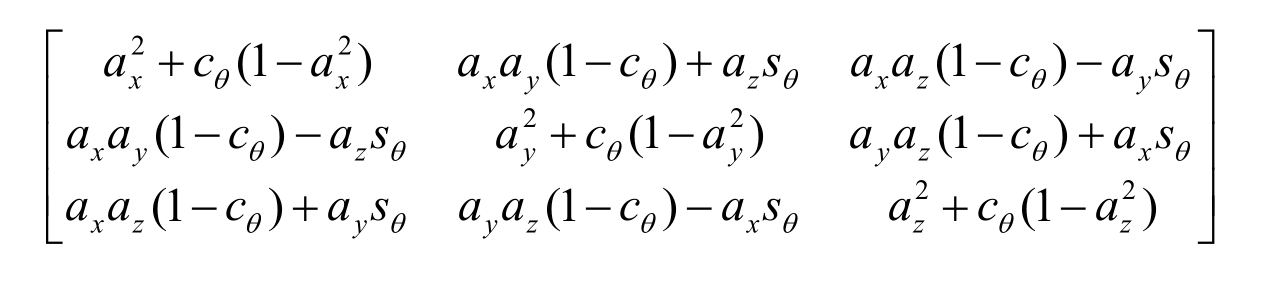
Axis Angle to Rotation Matrix

Quaternions

Cross product of two vectors:

\[\left[\begin{matrix}a_1 \\ a_2 \\ a_3\end{matrix}\right] \times \left[\begin{matrix}b_1 \\ b_2 \\ b_3\end{matrix}\right] = \left[\begin{matrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{matrix}\right]\]

Multiplication:

\[\begin{aligned} q_1 q_2 &= (w_1, \mathbf{v_1}) \times (w_2, \mathbf{v_2})\\ &= (w_1w_2 - \mathbf{v_1}\times\mathbf{v_2}, \quad\quad & \text{(Scalar)} \\ & w_1\mathbf{v_2} + w_2\mathbf{v_1} + \mathbf{v_1 \times v_2} ) \quad\quad & \text{(Vector)} \end{aligned}\]

FKIK

FK

\[T = L_\text{root}R_\text{root}L_1R_1 \dots L_kR_k\] 
void renderJoints(JOINT* joint, float*data, float scale) {	
	glPushMatrix();

	// translate
	if ( joint->parent == NULL ) { // is Root
		glTranslatef( data[0] * scale, data[1] * scale, data[2] * scale );
	} else {
		glTranslatef( joint->offset.x*scale, joint->offset.y*scale, joint->offset.z*scale );
	}

	// rotate
	for ( uint i=0; i<joint->channels.size(); i++ ) {
		CHANNEL *channel = joint->channels[i];
		if ( channel->type == X_ROTATION )
			glRotatef( data[channel->index], 1.0f, 0.0f, 0.0f );
		else if ( channel->type == Y_ROTATION )
			glRotatef( data[channel->index], 0.0f, 1.0f, 0.0f );
		else if ( channel->type == Z_ROTATION )
			glRotatef( data[channel->index], 0.0f, 0.0f, 1.0f );
	}

	// end site
	if ( joint->children.size() == 0 ) {
		renderSphere(joint->offset.x*scale, joint->offset.y*scale, joint->offset.z*scale,0.07);
	}
	if ( joint->children.size() == 1 ) {
		JOINT *  child = joint->children[ 0 ];
		renderSphere(child->offset.x*scale, child->offset.y*scale, child->offset.z*scale,0.07);
	}
	if ( joint->children.size() > 1 ) {
		float  center[ 3 ] = { 0.0f, 0.0f, 0.0f };
		for ( uint i=0; i<joint->children.size(); i++ )
		{
			JOINT *  child = joint->children[i];
			center[0] += child->offset.x;
			center[1] += child->offset.y;
			center[2] += child->offset.z;
		}
		center[0] /= joint->children.size() + 1;
		center[1] /= joint->children.size() + 1;
		center[2] /= joint->children.size() + 1;

		renderSphere(center[0]*scale, center[1]*scale, center[2]*scale,0.07);

		for ( uint i=0; i<joint->children.size(); i++ )
		{
			JOINT *  child = joint->children[i];
			renderSphere(child->offset.x*scale, child->offset.y*scale, child->offset.z*scale,0.07);
		}
	}

	// recursively render all joints
	for ( uint i=0; i<joint->children.size(); i++ )
	{
		renderJointsGL( joint->children[i], data, scale );
	}
	glPopMatrix();
}

Forward Kinematics

IK

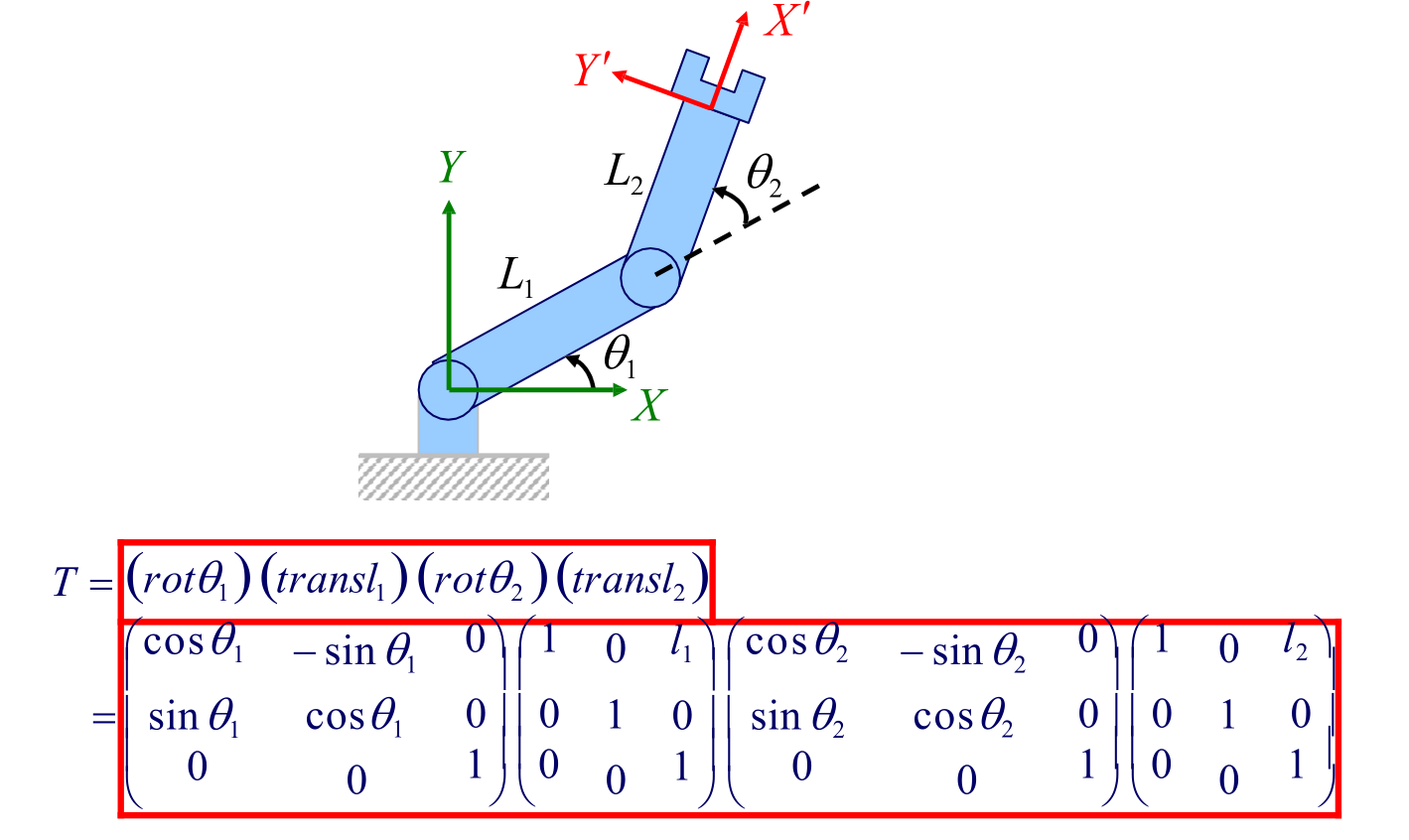
$a$ = axis of rotation

$r$ = distance vector from joint to end effector

$m$ = number of effectors

$v_e$ = velocity of end effector in one step

$\omega_e$ = angular velocity of end effector in one step

\[\mathbf{J} = \left[ \begin{matrix} a_1 \times r_1 & a_2 \times r_2 & \dots & a_m \times r_m \\ a_1 & a_2 & \dots & a_m \end{matrix} \right]\]

Solving: \(\begin{aligned} \left[ \begin{matrix} v_e \\ \omega _e \end{matrix} \right] &= \mathbf{J} \left[ \begin{matrix} \Delta\theta_1 \\ \vdots \\ \Delta\theta_m \end{matrix} \right] \\ \left[ \begin{matrix} \Delta\theta_1 \\ \vdots \\ \Delta\theta_m \end{matrix} \right] &= \mathbf{J^+} \left[ \begin{matrix} v_e \\ \omega _e \end{matrix} \right] \\ \theta_{t+1} &= \theta_t + \Delta \theta \end{aligned}\)

Moore-Penrose Pseudoinverse

Or see gradient descent (Jacobian Transpose).

Particle Systems

Hooke’s Law + Damping:

\[\]

Euler’s Method

\[\begin{aligned} v_t &= f(x_t, t)\\ x_{t+1} &= x_t + \Delta t \cdot f(x_t, t)\\ \end{aligned}\]

Midpoint method

\[\begin{aligned} x_{t+1/2} &= x_t + \frac{\delta t}{2} v_t\\ v_{t+1/2} &= f(x_{t+1/2}, t + 1/2)\\ x_{t+1} &= x_t + \Delta t \cdot v_{t+1/2}\\ \end{aligned}\]

Mass Spring Systems

\[x'' = M^{-1}(-\frac{\partial E}{\partial x} + F)\]

Mass Spring Systems