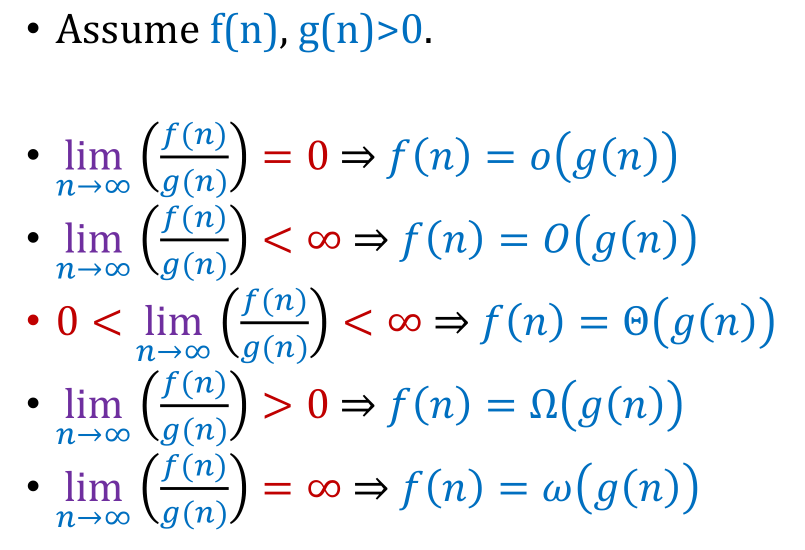
$\require{color}$

Word RAM Model

In the previous topic we went through the comparison and query models. These models had comparisons and queries respectively as the basic operational unit for their algorithms.

For the rest of the module we use the Word RAM model. This model assumes:

One processor (no concurrent operations)
Operates in binary
1 word = 4 bytes = 1 unit of RAM
Each logical operation (+, -, *, /, AND, OR, NOT) takes constant number of words

Input size: Depends on the problem. Can be either

Number of items in input (especially things involving lists)
Number of bits to represent the input (especially larger numbers)

Running time: counted by the number of basic instructions.

Asymptotic notations

O-notation, o-notation

For any $n > n_0$, $f(n) = O(g(n)) \Leftrightarrow 0 \le f(n) \le cg(n) \quad \text{for some } n_0, c>0$

Meanwhile o-notation is a tighter restriction: $f(n) = o(g(n)) \Leftrightarrow \text{for \textcolor{red}{any} } c>0, \quad 0 \le f(n) \textcolor{red}{<} cg(n)\text{ for some $n_0$ and } n > n_0$

Show $n^2 - n \neq o(n^2)$.

$\Omega$-notation, $\omega$-notation

For any $n > n_0$, $f(n) = \Omega(g(n)) \Leftrightarrow 0 \le cg(n) \le f(n) \quad \text{for some } n_0, c>0$

Meanwhile $\omega$-notation is a tighter restriction: $f(n) = \omega(g(n)) \Leftrightarrow \text{for \textcolor{red}{any} } c>0, \quad 0 \le cg(n) < f(n) \quad \text{for some $n_0$ and} , n > n_0$

Show $n^2 + n \neq \omega(n^2)$.

$\Theta$-notation

\[f(n) = \Theta(g(n)) \Leftrightarrow f(n) = O(g(n)) \text{ and } f(n) = \Omega(g(n))\]

or in other words,

\[f(n) = \Theta(g(n)) \Leftrightarrow 0 \le cg(n) \le f(n) \le dg(n) \quad \text{for some } n_0, d > c >0\]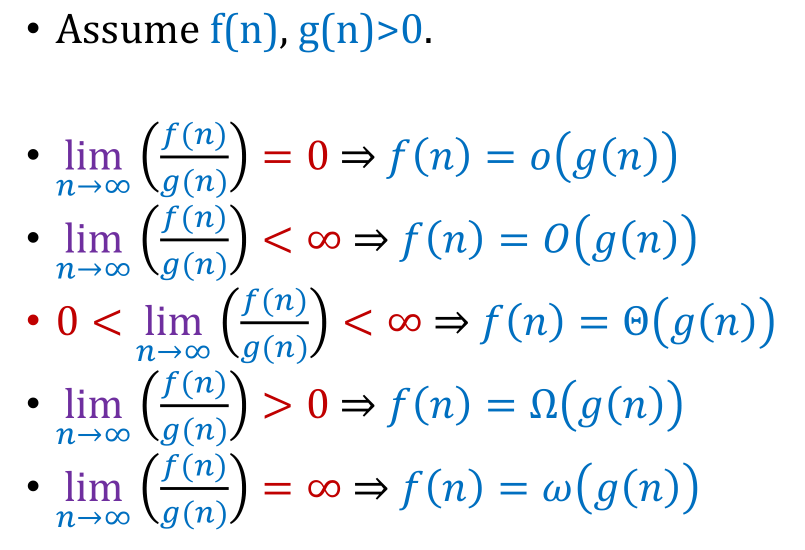

How to show an asymptotic bound

Epsilon-delta definition of limit $\lim_{x \rightarrow p} f(x) = L$.

For all $\epsilon > 0$,
there exists some $\delta > 0$
such that $0 < \mid x - p \mid < \delta \Rightarrow 0 < \mid f(x) - L \mid < \epsilon$.

Proving limits

Theorem. Show that $f(n) = o(g(n)) \Leftrightarrow \lim_{x \rightarrow \infty}\frac{f(n)}{g(n)}= 0$.

Proof. Given $\lim_{n \rightarrow \infty}\frac{f(n)}{g(n)}= 0$, for all $\epsilon > 0$, we have $\delta > 0$ such that

\[0 < \infty - n < \delta = \infty \Rightarrow \frac{f(n)}{g(n)} < \epsilon \Rightarrow f(n) < \epsilon g(n)\]

Setting $c = \epsilon$ and $n_0 = \delta$, we get for any $c > 0$, there is $n_0 > 0$ such that $f(n) < cg(n)$, which means by definition, $f(n) = o(g(n))$.

Similar argument can be made for rest of the statements.

Example

Show that $n^3 + 3n^2 + 4n + 1 = \omega(n^2)$.

\[\begin{aligned} &\lim_{n \rightarrow \infty} \frac{n^3 + 3n^2 + 4n + 1}{n^2} \\ =& \lim_{n \rightarrow \infty} \left( n + 3 + \frac{4}{n} + \frac{1}{n^2} \right)\\ =& \lim_{n \rightarrow \infty} (n) + 3 + 0 + 0 \\ =& \ \infty \\ \Rightarrow& \ n^3 + 3n^2 + 4n + 1 = \omega(n^2) \end{aligned}\]

Big-O Properties

Reflexivity

\[f(n) = O(f(n))\\ f(n) = \Omega(f(n))\\ f(n) = \Theta(f(n))\]

Transitivity

\[f(n) = O(g(n)) \text{ and } g(n) = O(h(n)) \Rightarrow f(n) = O(h(n))\]

Similar for other notations ($\Omega, \omega, o, \Theta$)

Symmetry

\[f(n) = \Theta(g(n)) \Leftrightarrow g(n) = \Theta(f(n))\]

Complementarity

\[f(n) = O(g(n)) \Leftrightarrow g(n) = \Omega(f(n))\\ f(n) = o(g(n)) \Leftrightarrow g(n) = \omega(f(n))\]