Network Security
Confidentiality: only sender and intended receiver can read message contents
- Cannot be viewed in transit or by wrong receiver
- Sender encrypt
- Receiver decrypt
Authentication: sender and receiver confirm each other’s identity
Message integrity: Readonly; message sholdn’t be altered without detection
Access and availability: Services must be accessible to all users.
Threat model: what are the capabilities of the attackers/threat?
- Eavesdropping (intercepting messages)
- Insertion of messages
- Impersonation via spoofing source address
Hijacking: “taking over” ongoing connection
- Denial of service (prevent serivce from being used by other authorized users)
- DDos: many different attackers attacking one server.
Terms
- $m$: plaintext message
- $K_A$: Alice’s encryption key
- $K_B$: Bob’s decryption key
- $K_A(m)$: ciphertext, encrypted with key $K_A$
- $m = K_B(K_A(m))$
How to break an encryption scheme
- Cipher-text only attack (attacker only has ciphertext)
- Brute force (go through all possibilities in the search space)
- Statistical analysis (attempts to shrink the search space)
- Known-plaintext attack (attacker has some plaintexts and their ciphertexts)
- Chosen-plaintext (attakcer can get ciphertext for chosen plaintext)
Cryptographies
Symmetric key cryptography
Bob and Aliceshare same symmetric key $K_A = K_B$.
Substitution cipher
e.g. Monoalphabetic cipher. Substitution of one letter for another.
Drawbacks:
- static mapping
- long key (all letters in alphabet)
- can be cracked by frequency analysis (matching common frequencies of letters)
Caesar’s cipher
Rotates the alphabet (with wraparound) by a certain amount $k$.
- Left rotation: ciphertext key needs to be rotated left by $k$ letters
- Right rotation: ciphertext key needs to be rotated right by $k$ letters
- Key: single number $k$
Drawbacks:
- static mapping
- can be cracked by frequency analysis (matching common frequencies of letters)
n-cipher approach
Start with $n$ substitution ciphers $M_1, M_2, \dots, M_n$. Establish a cyclic permutation of ciphers e.g. $M_4, M_1, M_3, M_6, M_5, M_2, M_4, M_1, \dots$
For each next plaintext symbol, use the next substitution pattern.
Key: n substitution ciphers, cyclic pattern
Encryption standards
Block cipher: applies deterministic algo with symmetric key to encrypt blocks of text of fixed length.
DES: Data Encryption Standard
- block cipher with cipher block chaining (block size 64-bit)
- No analytic attack
- 56-bit symmetric key is too insecure
- 3DES: 3x encryption with 3 different keys.
AES: Advanced Encryption Standard
- 128, 192, 256 bit keys
- Brute force (search space has $2^{256}$ keys as opposed to DES’ $2^{56}$)
Public Key Cryptography
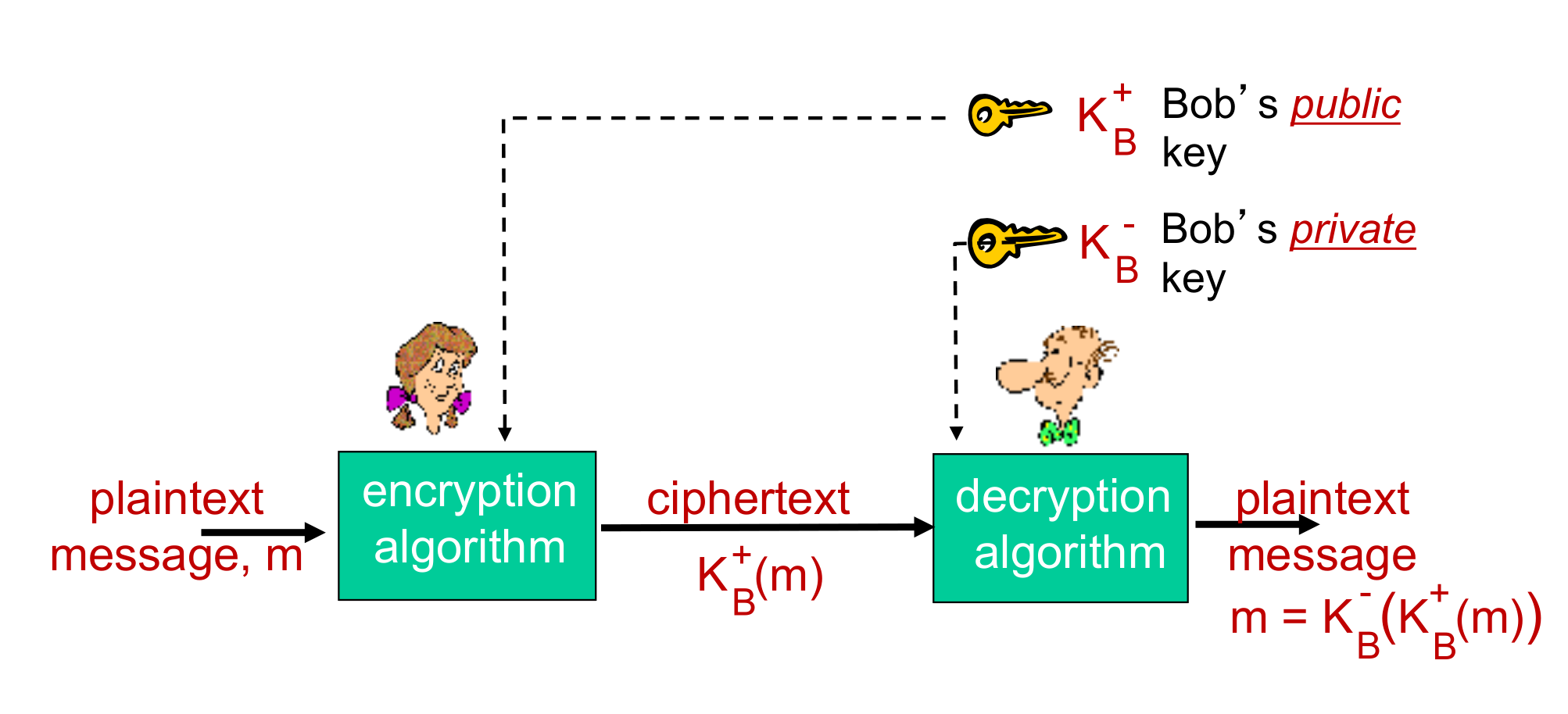
\[K_B^-(K_B^+(m)) = K_B^+(K_B^-(m)) = m\]
Given public key $K_B^+$, should be impossible to compute $K_B^-$.
RSA
Message = bit pattern = integer number.
Public private key generation
- Choose 2 large primes $p, q$ (e.g. 1024 bits each)
- $n = pq$, $z = (p-1)(q-1)$
- Choose $e$ such that $e < n$ and $e, z$ are coprime
- Choose $d$ such that $ed \mod z = 1$
- Public key = $(n, e)$. Private key = $(n, d)$.
RSA encryption, decryption
Obtain $(n,e), (n,d)$.
To encrypt message $m$: $c = m^e \mod n$.
To decrypt cipher $c$: $m = c^d \mod n$.
Proof:
Remember: $n = pq, z = (p-1)(q-1)$.
\[\begin{aligned}
m &= c^d \mod n\\
&= (m^e \mod n)^d \mod n\\
&= (m^{ed} \mod n) \mod n\\
&= (m^{(ed \mod z)} \mod n)\\
&= (m^1 \mod n)\\
&= m
\end{aligned}\]
Exponentiation is expensive computationally.
Why is RSA secure:
- How to obtain $d$ from $e$?
- Very hard as computing $d$ requires knowledge of the factors of $n$: $p$ and $q$
- Multiplication easy, factorization hard
Session keys
Use RSA to setup a secure encrypted channel, and exchange
a symmetric key.
Then use symmetric key to encrypt and decrypt.
Digital Signatures
Establishment of authorship/ownership of a document
Must be verifiable, non-forgeable: so recepient
can prove to owner that it is the intended recepient
and that it has received.
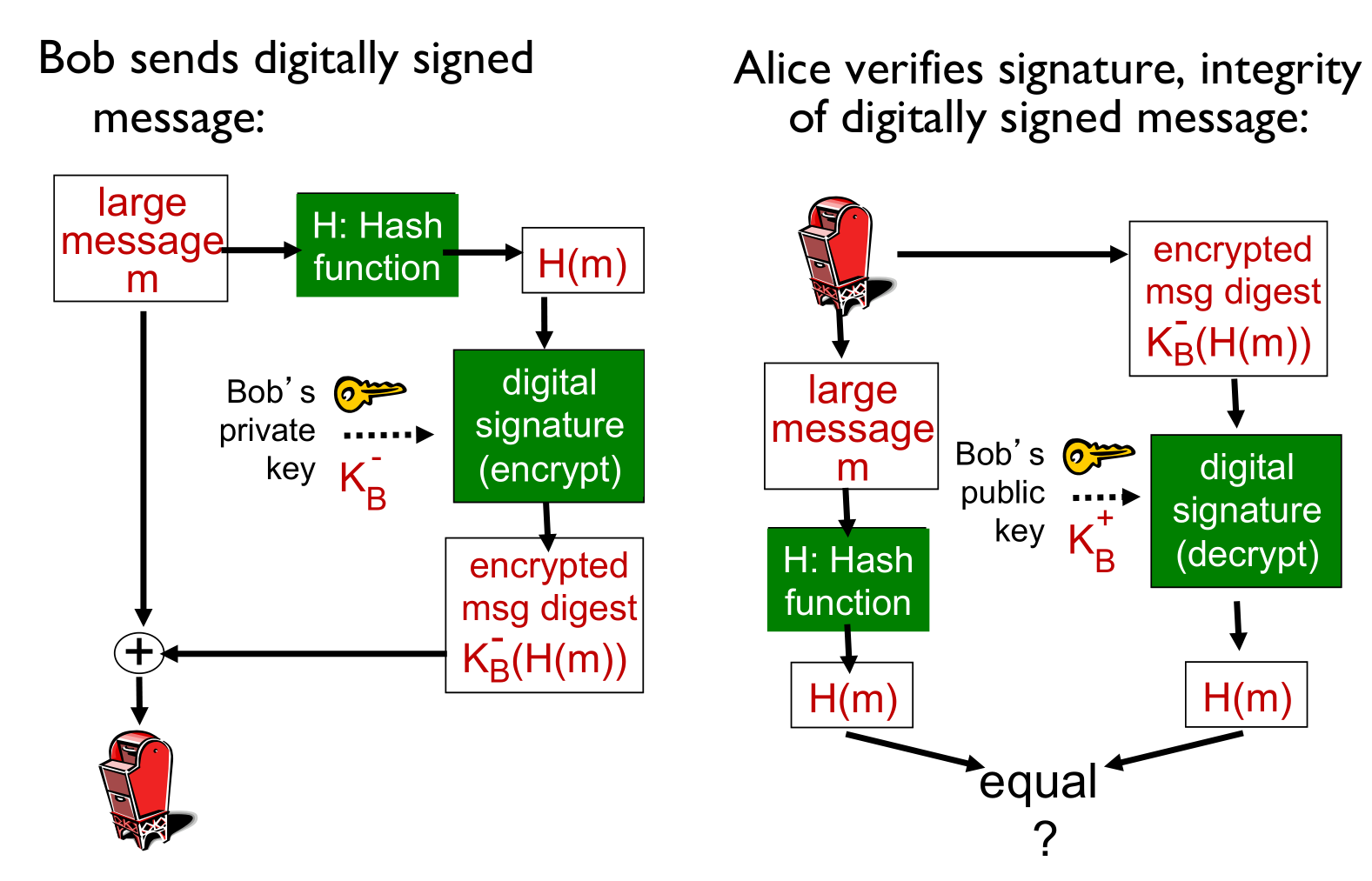
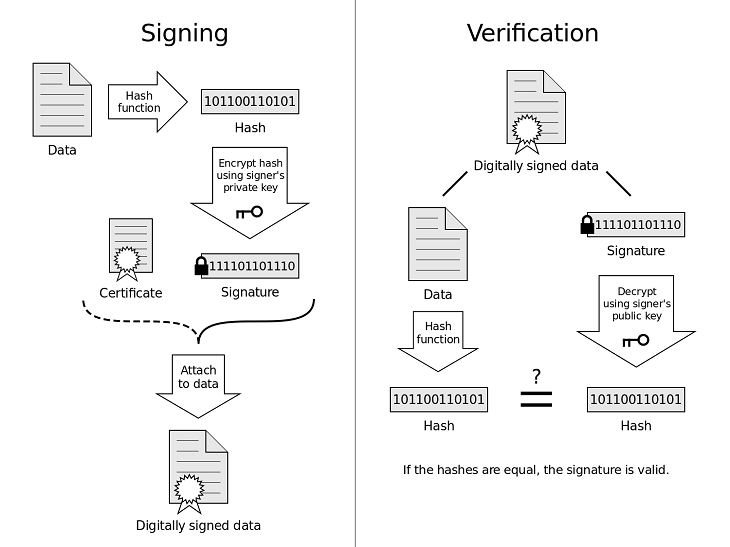
Simple digital signature
Bob sends message $m$ and encrypted with private key $K^-_B(m)$.
Alice receives both and checks if $m = K^+_B(K^-_B(m))$.
So we know whoever signed $m$ must have used Bob’s private key (non-repudiation).
Message digest
$m$ is run through a hash function $H$ which gives us a digest $H(m)$.
Cannot use 1s complement checksum (aka Internet Checksum):
has too many collisions.
Digest functions:
- MD5: 128-bits (short fixed length outputs)
- SHA-1
- SHA-256
Criteria: Small change in input should lead to large change in digest.
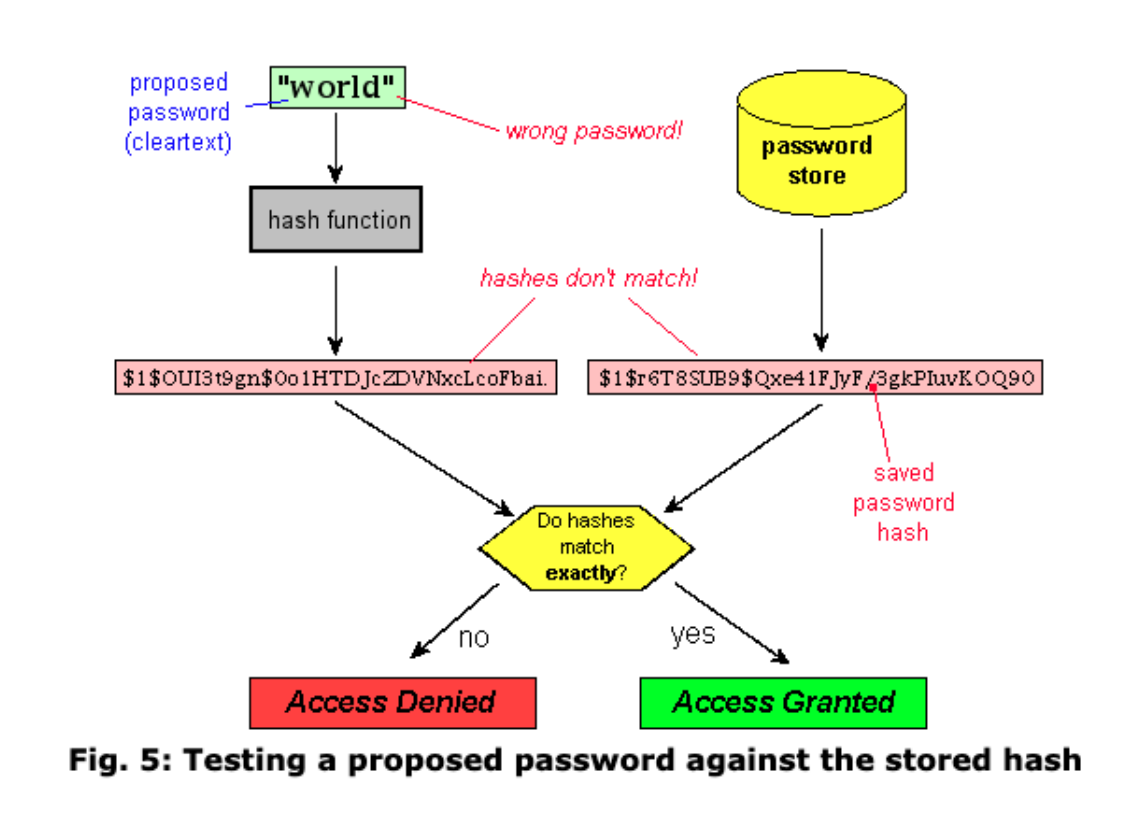
Example – Password storage:
- database should store hashed password
- app hashes password input
- server compares hashed password to stored hash
Certification Authorities
Public keys have to be known! Otherwise someone can
replace the public key and say its mine when its really theirs (Impersonation).

Hence we have CAs
- Person E registers public key with CA.
- CA provides certificate binding E to the public key submitted
- Certificate containing E’s public key to be signed by CA.
- Person F wants public key.
- Get Person E’s certificate
- F apply CA’s public key to E’s certificate to get B’s public key.
TLS Handshake
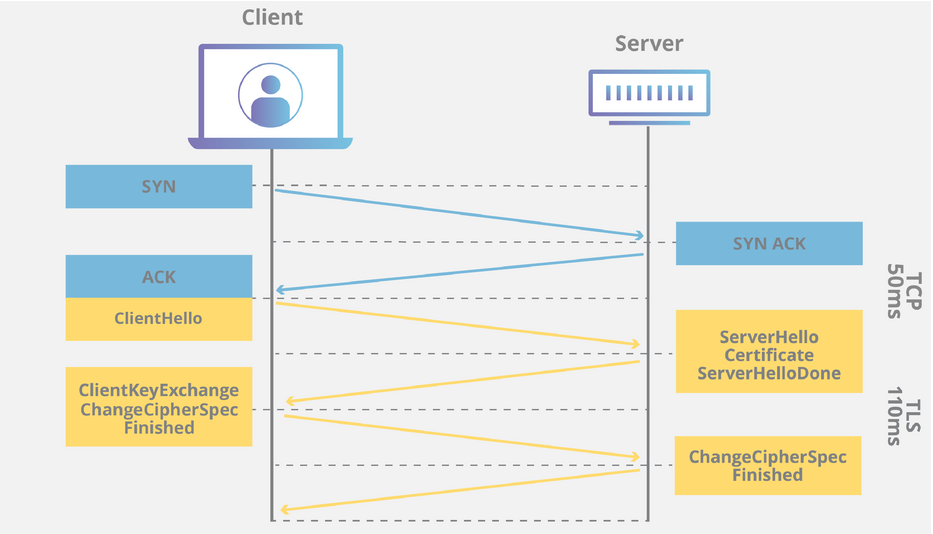
- Client hello: Client sends client random
- Server hello: Server sends SSL cert + server random
- Authentication: Client verifies SSL cert with the CA’s public key.
- Premaster secret: Client sends a byte string with the public key extracted from the SSL cert
- Server decrypts secret with private key.
- Session keys: Both client and server generate session keys from client random, server random and premaster secret.
- Both client and server should arrive at the same results.
- Client and server send each other “finished” message encrypted with their session keys
- Handshake complete.
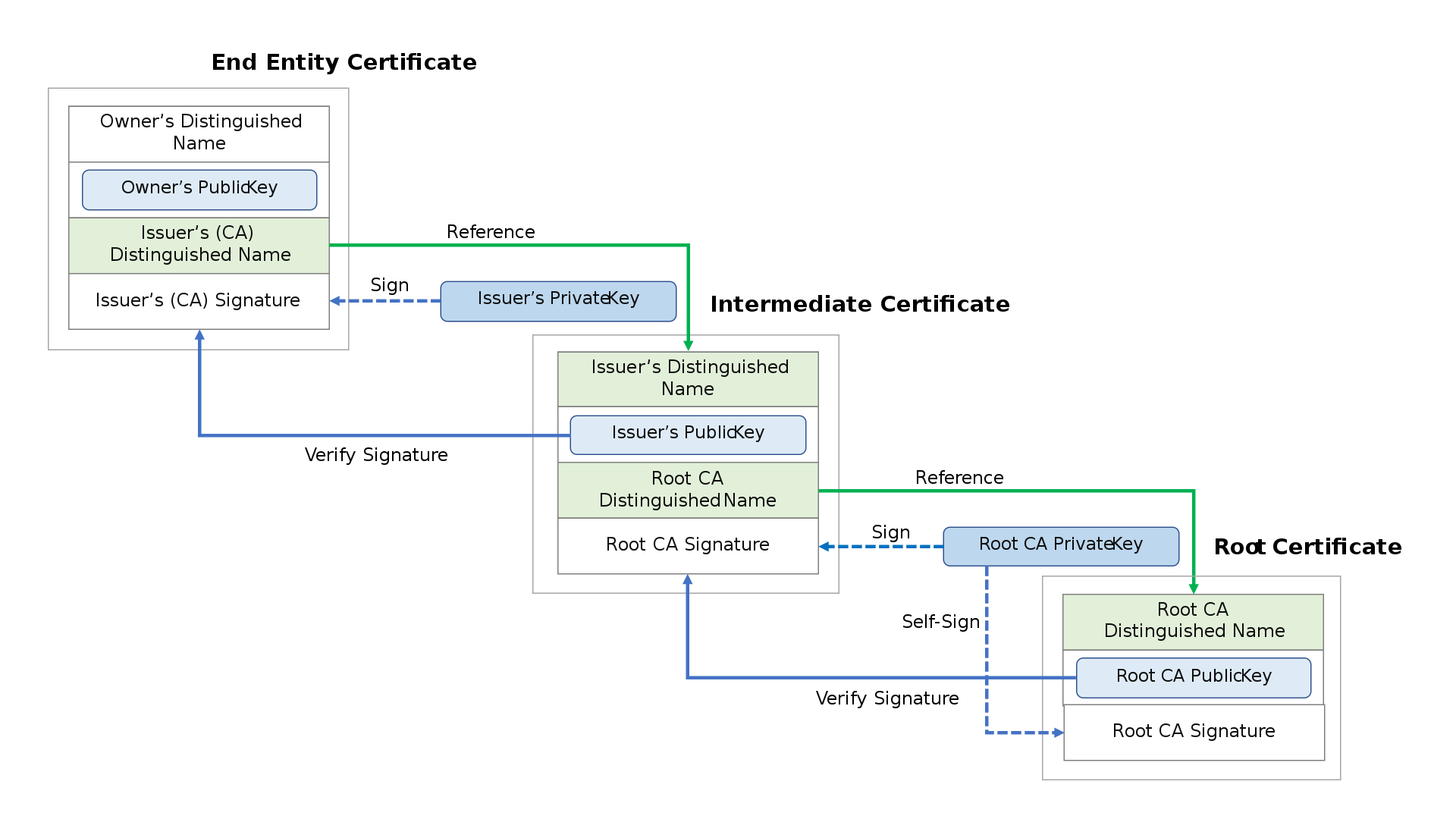
Chain of Trust
From end entity/domain, to Certification Authorities, to Root Certification Authorities
Virtual Private Networks
Firewalls
Isolates internal network, allowing some packets to pass but block others.
- Prevent DoS attacks
- Prevent illegal modification of data
- Authorization only
Three types of firewalls
Setting up policy rules, with which packets and filtered and dropped/forward if necessary.
Packet filtering types:
- stateless: Analyses per packet individually, forward/drop based on
- Source/Dest IP
- TCP/UDP source/dest port numbers
- ICMP message type
- stateful: Track status of each TCP connection,
- Tracking connection setup (SYN) and teardown (FIN)
- application gateways







