$\require{color}$

Photorealistic rendering

Inputs (camera, geometry, lighting, materials) must all be accurate and detailed enough to support.

Material Appearances

Reflection: BRDF (Bidirectional Reflection Distribution Function)
Transmission: BTDF (Bidirectional Transmission Distribution Function)

Reflection by local reflection models such as

Phong (empirical, not physically based)
Cook-Torrance (physically based)

Local reflection models: rs between

One light source
A single surface point
The view point
No interactions between other objects.

Global illumination considers all light sources and surfaces, inter-reflections and shadows.

Radiometry

Radiometry: Physical measurement of light/radiation energy

Summary:

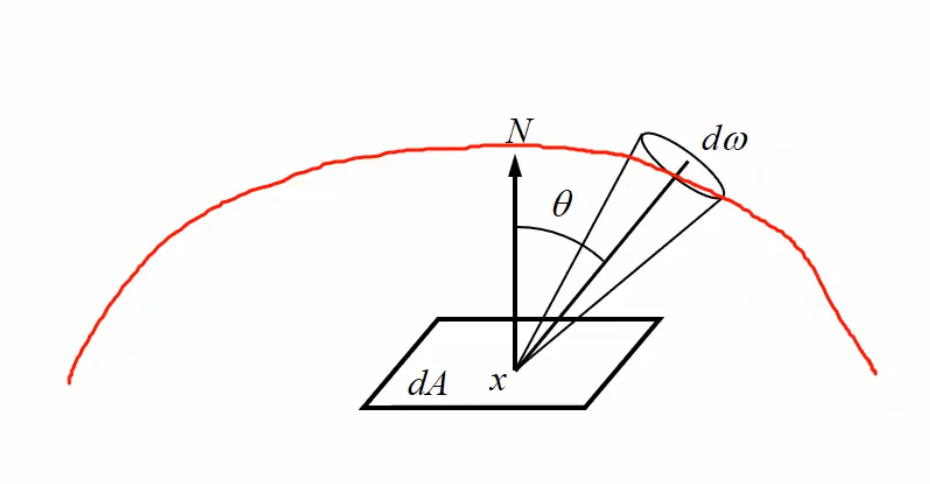
\[\begin{aligned} \text{Radiant Power } \Phi &: \text{light energy over unit time} \\ \text{Irradiance } E &= \frac{d \Phi}{dA} = \text{incident power per unit surface area}\\ &= \int_\Omega L(x \leftarrow \Psi) (N \cdot \Psi) d\omega_\Psi \\ \text{Radiosity } B &= \frac{d \Phi}{dA} = \text{outgoing power per unit surface area}\\ &= \int_\Omega L(x \rightarrow \Theta) (N \cdot \Theta) d\omega_\Theta \\ \text{Radiosity } L &= \frac{d^2 \Phi}{d\omega \cdot dA \cos \theta} \end{aligned}\]

Radiant power and radiance:

\[\Phi = \int_A \int_\Omega L(x \rightarrow \Theta) cos \theta d\omega_\Theta dA_x\]

Radiance $L$:

“Intensity” of light
Radiant power per unit projected surface area per unit solid angle
- Solid angle: The apparent size of the light source from the center view point.
- Solid angle: (in steradians) the Sphere surface area intercepted by a cone, divided by square of the sphere’s radius $r$.
- Solid angle: $2\pi r^2 = 2\pi$
- Projected surface area: From an oblique projection angle, the surface area that the light hits changes
- Projected surface area: surface area $\times \cos \theta$
- The reason being we don’t want the size of the light source (solid angle) and direction of the light (projected surface area) to affect the computation of radiance.
$W/(srm^2)$

Radiometic quantities’ relationship

Radiometric quantities vary with wavelength, and is perception independent.

Radiance is invariant along straight paths (assuming no medium), and sensors are sensitive to radiance. Together these explain why color/brightness of an object seems to not change with distance.

Example: Diffuse emitter

Emits equal radiance $L$ in all directions.

\[\begin{aligned} B(x) &= \int_\Omega L(x \rightarrow \Theta) \cos \theta d \omega_\Theta\\ &= L \int_\Omega \cos \theta d \omega_\Theta \quad \text{(L is constant.)}\\ &= L \int_{\theta = 0}^{\pi/2} \int_{\phi = 0}^{2\pi} \cos \theta \sin \theta d\theta d\phi \\ & \text{(longitudinal $\theta$, latitudinal (equatorial) $\phi$.)}\\ &= \textcolor{red}{L\pi} \end{aligned}\]

Bidirectional Reflection Distribution Function (BDRF)

Describes the amount of incident light reflected in exitant direction.

BRDF = Outgoing radiance $L$ $\div$ Incoming irradiance $E$

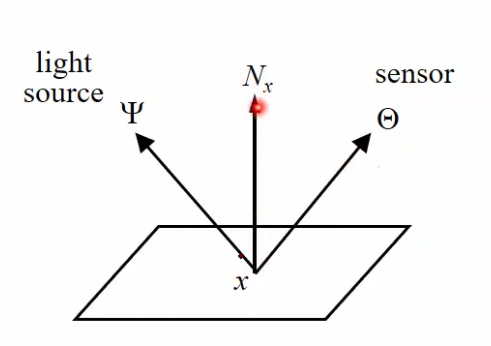
\[\text{BRDF}, f_r (x, \Psi \rightarrow \Theta) = \frac{dL(x \rightarrow \Theta)}{dE(x \leftarrow \Psi)}\\ = \frac{dL(x \rightarrow \Theta)}{L(x \leftarrow \Psi)(N_x \cdot \Psi) d\omega_\Psi}\]

$\Psi$ is incident/incoming light source direction, $\Theta$ is outgoing light.

Implications:

BRDF is independent on solid angle of incoming irradiance.
$\frac{dL}{dA} \div \frac{dE}{dA} = \frac{dL}{dE}$

Assumptions:

Frequency of light unchanged (no fluorescence)
Light reflected instantaneously (no phosphorescence)
No subsurface scattering

Range: Any non-negative value

Dimensionality: 4D (incoming and outgoing each contribute two dimensions)

The requirements for physically feasible BRDF are below:

Note about $R$: Occasionally the reflection ray $R = 2(N \cdot \Psi)N - \Psi$ would be included the BRDF. Remember to expand and replace all relevant values.

Helmholtz reciprocity

BRDF is symmetric.

\[f(x, \Psi \rightarrow \Theta) = f(x, \Psi \leftarrow \Theta)\]

Energy conservation

Total power reflected in all directions must be equal to or less than incident power.

\[\int_\Omega f_r(x, \Psi \rightarrow \Theta)(N_x \cdot \Theta)d_\omega \le 1\]

Isotropic

If the BRDF is independent of the incident light $\Psi$’s azimuth angle, it would not include any angle formed by $\Psi$ and any fixed vector (e.g. the tangent of a hair strand.)

Cook Torrance model cannot represent anisotropic (not isotropic) models.

Example BRDFs

Diffuse surface/reflector
1. $f_x(\Psi \rightarrow \Theta) = \frac{k_d}{\pi}$
2. $k_d$ diffuse reflectance (aka albedo)
Perfect mirror reflector
1. BRDF is 0 in all directions except
2. Reflected direction (infinite)
3. $\int_\Omega f_r(x\Psi \rightarrow \Theta)(N_x \cdot \Theta)d_\omega = 1$

Example shading models

Lambertian shading model

\[f_r(x, \Psi \leftirhgtarrow \Theta) = \frac{k_d}{\pi}\]

Energy conserving? Yes, if $0 \le k_{d,r}, k_{d,g}, k_{d,b} \le 1$
Satisfying Helmhotz yes.

Phong model

\[f_r(x, \Psi \leftright \Theta) = k_s \frac{n+8}{8\pi}(R\cdot \Theta)^n + \frac{k_d}{\pi}\]

Energy conserving? Yes, if $0 \le k_{s,i} + k_{d,i} \le 1$
Satisfying Helmhotz yes.

Blinn-Phong model

\[f_r(x, \Psi \leftright \Theta) = k_s \frac{n+8}{8\pi}(\textcolor{red}{N \cdot H})^n + \frac{k_d}{\pi}\]

Energy conserving? Yes, if $0 \le k_{s,i} + k_{d,i} \le 1$
Satisfying Helmhotz yes as incoming/outgoing is symmetrical about $H$

Phong model limitations

Objects have a plastic-like appearance (diffuse surface + lacquered)

Cannot simulate metallic appearance, where intensity and color of the specular highlights depends on angle of incoming light.

No fresnel effects

Metallic surface

The thinner the lobe, the closer to perfect mirror reflection we have, which implies more shininess.

This demonstrates the difference in BRDF when it comes to different wavelengths of light.

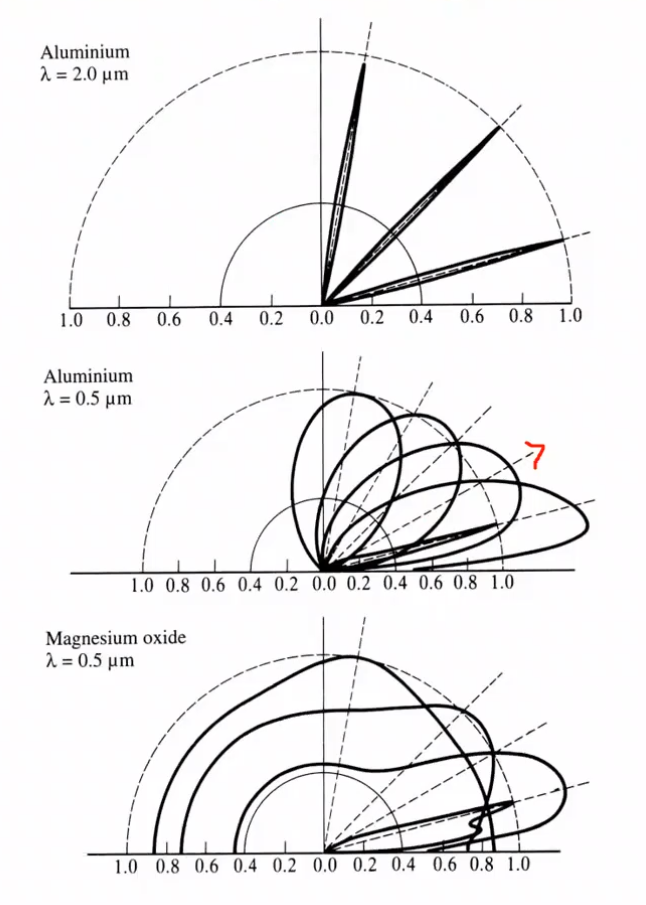
Off specular reflection: the highest intensity may not be at the reflection angle.

Fresnel Equation

The ratio of reflected to transmitted light energy:

\[F = \frac{1}{2} \left( \frac{\sin^2(\phi - \theta)}{\sin^2(\phi + \theta)} + \frac{\tan^2(\phi - \theta)}{\tan^2(\phi + \theta)} \right)\]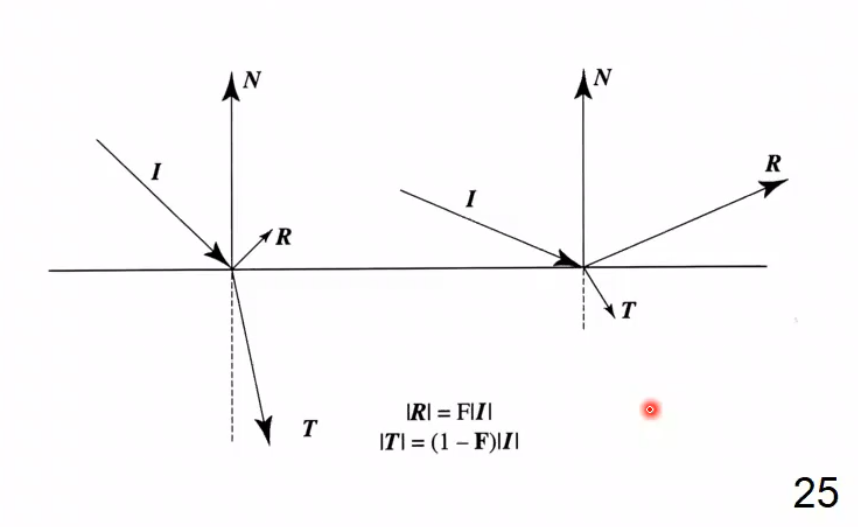

Schlick’s Approximation

\[F = f + (1 - f) (1 - L \cdot N)^5\]

where $f = \frac{(1 - n_1/n_2)^2}{(1 + n_1/n_2)^2}$

Cook-Torrance Reflection Model

Only models the specular component (which is added to the normally computed diffuse model.)

\[f_r(x,\Psi \leftrightarrow \Theta) = \frac{D(\alpha)GF}{(N\cdot\Psi)(N\cdot\Theta)\pi} + \frac{k_d}{\pi}\]

$D(\alpha)$: Micro-geometry term

$\alpha$ is the angle between $N, H$, $H = \frac{L + V}{ L + V }$.
Gives the proportion of microfacets that mirror reflect this light in direction V.
$m = \sigma$ standard deviation: controls mean surface roughness.

\[D(\alpha) = ke^{-(\alpha/m)^2}\]

$G$: Shadowing/Masking term

$G_s = (N \cdot H)(N \cdot V)/(V \cdot H)$
$G_m = (N \cdot H)(N \cdot L)/(V \cdot H)$

\[G = \min{1, G_s, G_m}\]

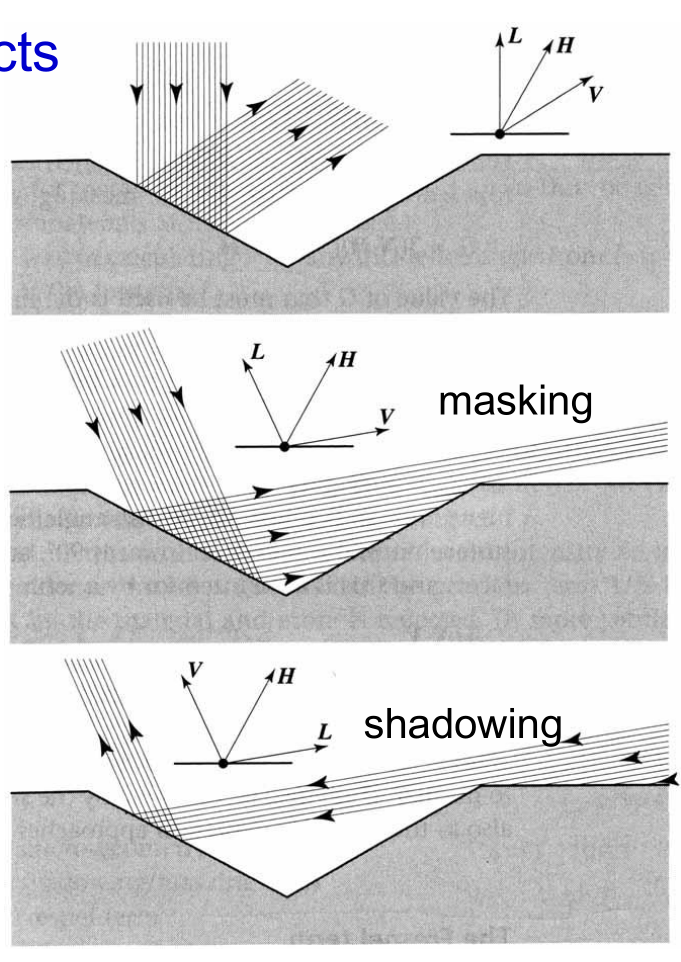
$F$: Fresnel term (see above)

$1/(N \cdot V)$ to account for glare.

Isotropic

(See above) Independent of azimuthal (equatorial) angle $\phi$.

\[f_r(x, (\theta_i, \phi_i) \leftrightarrow (\theta_o, \phi_o)) = f_r(x, (\theta_i, 0) \leftrightarrow (\theta_o, \phi_o - \phi_i))\]