

Vertex shader: transform the vertex position and vertex normal (inputs) to eye space as per normal
Fragment shader:
// Light position from behind the camera
const vec4 LightPosition = vec4(0.0, 0.0, 1.0, 0.0);
const vec3 MyColor = vec3(...);
void main() {
vec3 viewVec = -normalize(ecPosition);
vec3 necNormal = normalise(ecNormal);
// set the unit light vector.
vec3 lightVec;
if (LightPosition.w == 0.0)
lightVec = normalize(LightPosition.xyz);
else lightVec = normalize(LightPosition.xyz - ecPosition);
float N_dot_L = max(0.0, dot(necNormal, lightVec));
// split N_dot_L into 4 thresholds
if (N_dot_L < 0.5) FragColor = vec4(vec3(0.0), 1.0);
else if (N_dot_L < 0.7) FragColor = vec4(0.5 * MyColor, 1.0);
else if (N_dot_L < 0.9) FragColor = vec4(1.0 * MyColor, 1.0);
else FragColor = vec4(1.0);
}
Vertex shader: Transform vertex position, normal and tangent as well to eye space.
Fragment shader: With the interpolated normals and tangents,
// Computing perturbed normal
// Get where fragment is in BumpDensity * BumpDensity grid
vec2 c = BumpDensity * texCoord.st;
// Where is the fragment in relation to its bump
vec2 p = fract(c) - vec2(0.5);
float sqrDist = p.x * p.x + p.y * p.y;
if (sqrDist >= BumpRadius*BumpRadius) p = vec2(0.0);
// The perturbed normal vector in tangent space.
vec3 tanPerturbedNormal = normalize( vec3(p.x, p.y, 1.0) );
// The perturbed normal vector in eye space.
vec3 ecPerturbedNormal =
tanPerturbedNormal.x * T +
tanPerturbedNormal.y * B +
tanPerturbedNormal.z * N;
Can instead get perturbation vectors from a texture map aka normal map.
Each texel contains the 3 perturbation vector components in the RGB channels.
Need to map $[- 1, 1] \mapsto [0, 1]$ bijectively. Hence unperturbed normal $[0, 0, 1] \mapsto [0.5, 0.5, 1]$ in normal map.
How do we derive the tangent vector from texture coordinates:
void compute_tangent_vectors( vec3 N, vec3 p, vec2 uv, out vec3 T, out vec3 B )
{
// get edge vectors of the pixel triangle
vec3 dp1 = dFdx( p );
vec3 dp2 = dFdy( p );
vec2 duv1 = dFdx( uv );
vec2 duv2 = dFdy( uv );
// solve the linear system
vec3 dp2perp = cross( dp2, N );
vec3 dp1perp = cross( N, dp1 );
T = normalize( dp2perp * duv1.x + dp1perp * duv2.x ); // Tangent vector
B = normalize( dp2perp * duv1.y + dp1perp * duv2.y ); // Binormal vector
}
Here dFdx and dFdy return the partial derivatives of provided argument p with respect to the x and y coordinate respectively.
See “Followup: Normal Mapping Without Precomputed Tangents”.
Store an image to a cubemap, to be mapped as the environment to object. Then using the reflection as texture coordinates.
Similar to reflection.
refract in GLSLLimitation: Rays are not refracted at the 2nd exit point.

As view ray approaches grazing angle (almost parallel to tangent, perpendicular to normal): reflected light increases.
$F$ is the proportion of energy reflected back into the viewpoint. \(F = \frac{1}{2}\left( \frac{\sin^2(\phi - \theta)}{\sin^2(\phi + \theta)} + \frac{\tan^2(\phi - \theta)}{\tan^2(\phi + \theta)}\right)\) Where $\phi$ is the angle of incidence, $\theta$ is the angle of refraction and by Snell’s law, $\sin \theta = \sin \phi / \mu$ where $\mu$ is the refractive index ratio.
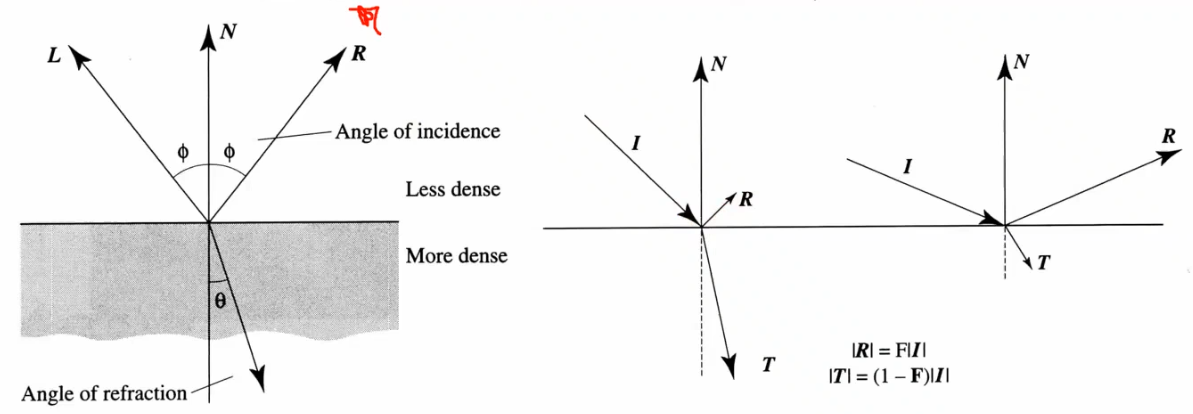
Assumptions: Unpolarized incoming light, dielectric surface. Refractive index is dependent on wavelength $\lambda$.
Problem: The computation is expensive.
where $f = \left(\frac{1.0 - n_1/n_2}{1.0 + n_1/n_2}\right)^2$.
Vertex shader:
// Compile time constants
const float Eta = 0.66; // n1/n2
const float FresnelPower = 5.0;
const float f = ((1.0 - Eta)*(1.0 - Eta))/((1.0 + Eta)*(1.0 + Eta));
out vec3 Reflect;
out vec3 Refract;
out float Ratio;
void main() {
// ... compute ecPosition
vec3 i = normalize(ecPosition3);
vec3 n = normalize(NormalMatrix * vNormal);
Ratio = f + (1.0 - f) * pow( 1.0 - dot(-i, v) , FresnelPower);
Refract = refract(i, n, Eta);
Reflect = reflect(i, n);
}
Fragment shader:
void main() {
vec3 reflectColor = vec3(texture(env, Reflect));
vec3 refractColor = vec3(texture(env, Refract));
vec3 color = mix(reflectColor, refractColor, Ratio);
FragColor = vec4(color, 1.0);
}
Different refractive indices for R, G, B channels.
Vertex shader:
// Compile time constants
const float EtaR = 0.65; // for red
const float EtaG = 0.67; // for green
const float EtaB = 0.69; // for blue
const float FresnelPower = 5.0;
const float f = ((1.0 - EtaG)*(1.0 - EtaG))/((1.0 + EtaG)*(1.0 + EtaG));
// Approximately the same for all 3, so use median Eta (green).
out vec3 Reflect;
out vec3 RefractR, RefractG, RefractB; // calculate thrice.
out float Ratio;
Fragment Shader:
refractColor.r = texture(Cubemap, RefractR).r; // only red channel.
refractColor.g = texture(Cubemap, RefractR).g; // only green channel.
refractColor.b = texture(Cubemap, RefractR).b; // only blue channel.