$\require{color}$
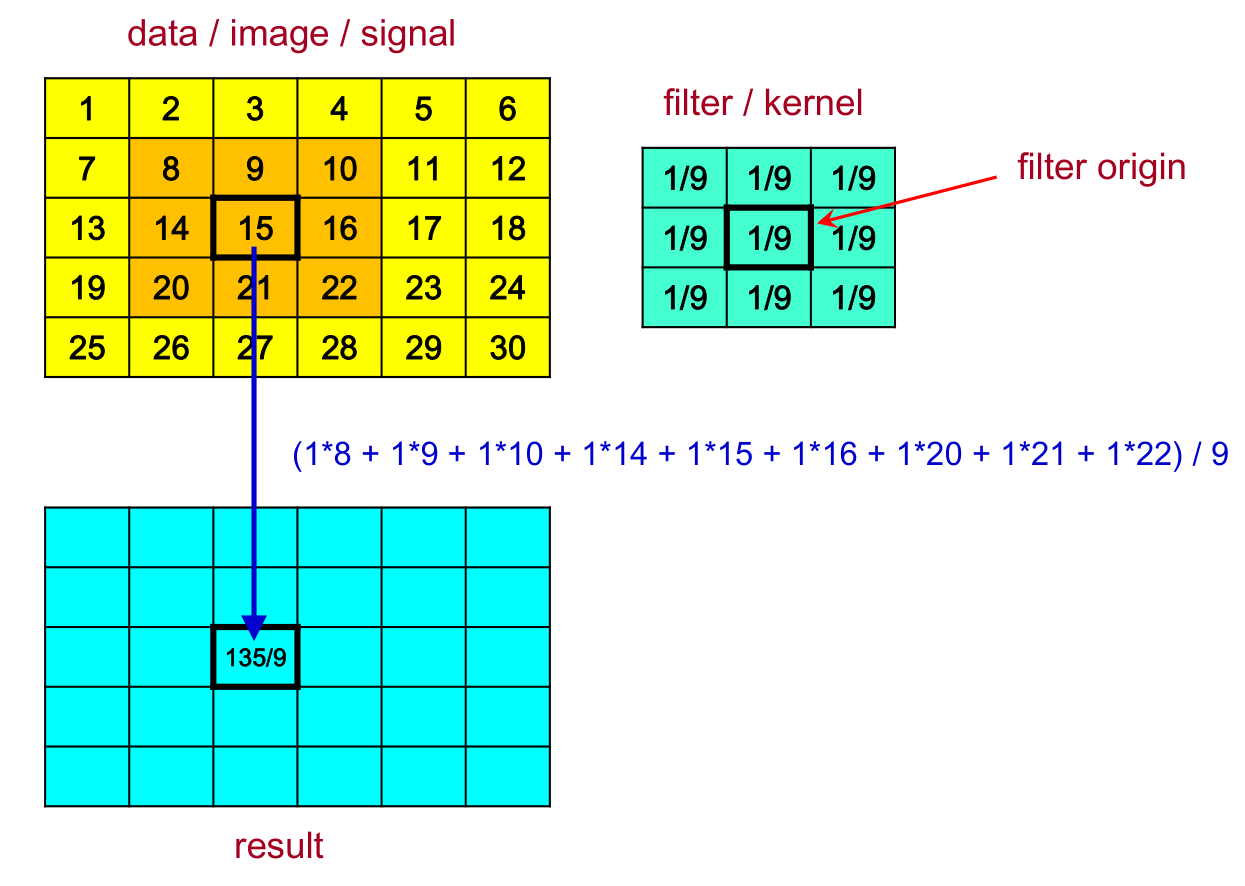
Replaces a pixel’s value with a weighted sum of pixels in the neighbourhood of the pixel (e.g. 3x3). A convolution filter/kernel is a matrix that specifies the weights.

texelFetch to read from texture mapsivec2 pix = ivec2(gl_FragCoord.xy);
// Weight[x] is the value of the kernel at position x
vec4 sum = texelFetch(RenderTex, pix, 0) * Weight[0];
// Horizontal convolution kernel
for (int i = 1; i < 5; i++) {
sum += texelFetchOffset(RenderTex, pix, 0, ivec2(0, PixOffset[i])) * Weight[i];
sum += texelFetchOffset(RenderTex, pix, 0, ivec2(0, -PixOffset[i])) * Weight[i];
}
FragColor = sum;
texture |
texelFetch |
|---|---|
| handles filtering | no filtering, directly accesses a texel from image |
| via texture coordinates $\in(0,1)$ | via texel coordinates $(0, w \text{or} h)$ |
Note on fragment position:
Sobel operator. Apply $S_x, S_y$ to the 3x3 pixel grid.
\[S_x = \left[ \begin{matrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{matrix} \right], \quad S_y = \left[ \begin{matrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \\ \end{matrix} \right]\]If $\textcolor{red}{g = \sqrt{s_x^2 + s_y^2} > d}$ where $d$ is some threshold, then it is an edge pixel.
passNum to 1passNum to 2texelFetchOffset(texture, pixCoord, 0, offset)texture2D.// rounding down xy clip coords to get the pixel position (screenfilling quad.)
ivec2 pix = ivec2(gl_FragCoord.xy);
// texel coordinates of texture map == fragment position in output image.
// the texel values from the render texture.
float s00 = luminance(texelFetchOffset(RenderTex, pix, 0, ivec2(-1, 1)).rgb)
...
float s22 = luminance(texelFetchOffset(RenderTex, pix, 0, ivec2(1, -1)).rgb)
float sx = s00 + 2 * s10 + s20 - (s02 + 2 * s12 + s22);
float sy = s00 + 2 * s01 + s02 - (s20 + 2 * s21 + s22);
float g = sx * sx + sy * sy;
Lens blur/bloom useful.
The Gaussian Kernel/Filter is defined as such ($\sigma$ is the standard deviation):
\[G(x,y) = \frac{1}{2\pi\sigma} e^{-\frac{x^2 + y^2}{2\sigma^2}}\]We exploit that it is a product of two 1D Gaussian functions (2D gaussian blur is separable), i.e. $G(x,y) = G(x)G(y)$, where
\[G(x) = \frac{1}{\sqrt{2\pi\sigma}} e^{-\frac{x^2}{2\sigma^2}}\]Gaussian kernel weights should add up to 1.
Hence the 2D digital convolution has the following 9x9 kernel ($C_{a,b}$ is the original ):
\[\begin{aligned} C'_{l,m} &= \sum_{i= -4}^4 \sum_{j=-4}^4 \frac{G(i,j)}{k} C_{l+i, m+j} \\ &= \sum_{i= -4}^4 \frac{G(i)}{k} \sum_{j=-4}^4 \frac{G(j)}{k} C_{l+i, m+j} \\ \end{aligned}\]where $k = \sum_{i=-4}^4 G(i)$ to ensure weights sum to one.
uniform int PassNum;
// the gaussian filter pixel offsets. needs to be declared here
// cos texelFetchOffset only works with stuff known at compile time.
uniform int PixOffset[5] = int[](0, 1, 2, 3, 4);
// Gaussian filter weights
uniform float Weight[5];
// Results of first and second pass
uniform sampler2D RenderTex;
layout (location = 0) out vec4 FragColor;
void pass1() {
// Lighting computation
FragColor = ...;
}
void pass2() {
ivec2 pix = ivec2(gl_FragCoord.xy);
// Weight[0] is the center value of the kernel
vec4 sum = texelFetch(RenderTex, pix, 0) * Weight[0];
//
for (int i = 1; i < 5; i++) {
sum += texelFetchOffset(RenderTex, pix, 0, ivec2(0, PixOffset[i])) * Weight[i];
sum += texelFetchOffset(RenderTex, pix, 0, ivec2(0, -PixOffset[i])) * Weight[i];
}
FragColor = sum;
}
// pass 3 is the same but instead ivec2(+-PixOffset[i], 0)
How to compute Gassian blur? No need for the constant $\frac{1}{\sqrt{2\pi\sigma}}$.
char uniName[20];
float weights[5], sum, sigma2 = 4.0f;
// Compute and sum the weights
weights[0] = gauss(0, sigma2); // gauss is the 1D Gaussian function
sum = weights[0];
for (int i = 1; i < 5; i++) {
weights[i] = gauss(i, sigma2);
sum += 2 * weights[i];
}
for (int = 0; i < 5; i++) {
snprintf(uniName, 20, "Weight[%d]", i);
prog.setUniform(uniName, weights[i] / sum);
}